Quoted from "Sir_Flauschi28"

saya also irgendwie kommst du mir ein bisl wie ein klugscheisser vor !
meine funktion lautet e^x - 2x= 0, sorry aber ich hab ka wie man so schöne hochzahlen tippt .
:-[
@bulch
wie berechnet man denn die nullstellen? du scheinst ja zu wissen wie es geht .

mfg Henning

Warum sagst du sowas? Find ich jetzt echt fies von dir. > Wir versuchen dir zu helfen und dann sowas. Es ist doch nunmal Fakt, dass eine Nullstelle kein Punkt ist. Bei uns gibt es zumindest immer Punktabzug, wenn du statt ner Nullstelle einen Punkt hinschreibst.

Und da du sagtest, es müsse eine Nullstelle da sein, dacht ich mir halt, du hättest dich nochmal verschrieben.

Ich weiß auch wie man eine Nullstelle berechnet. Bin ja ned aus Spaß im Mathe-LK der 12.

Sieh dir doch mal den Graph an:






---------------------------

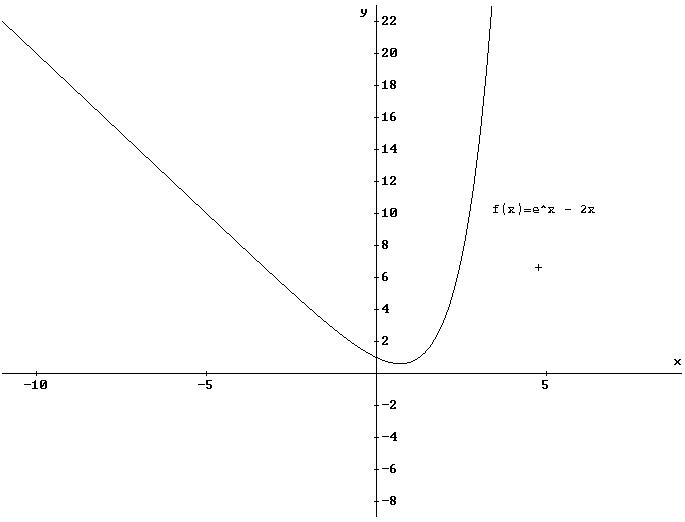
e^x - 2x = 0 |+2x
e^x = 2x |ln
x * ln(e) = ln(2x)
x = ln(2x)

f(x) = x
g(x) = ln(2x)

f'(x) = 1 >>>> immer Anstieg 1
g'(x) = 1/x >>> nur an der Stelle x = 1 ist der Anstieg 1

f(1) = 1
g(1) = 0,69

Es gibt keinen Berührpunkt mit der X-Achse.

Jetzt muss man nur noch rechnerisch nachweise, dass es neben dem Berührpunkt auch keinen Schnittpunkt mit der X-Achse gibt.

Der Graph von g liegt unterhalb von f. Mit zunehmendem x sinkt der Anstieg von g. Wenn x gegen Null strebt wird der Anstieg von g immer größer, der Funktionswert von g wird unendlich klein. Da f(x) = x jedoch durch den Ursprung verläuft und immer den Anstieg 1 hat, wenn g(x) schon weit unter dem Anstieg 1 ist, können sie die Graphen von g und f nicht schneiden.

Es gibt folglich auch keine Nullstelle für e^x - 2x .

MfG

Besser hätte ich es auch nicht Erklären können.
Hätte ich Webspace hätte ich dir schon am Anfang den Funktionsgraphen gezeigt.
M-LK 13

e^x-2x ist nie 0, was doch wohl zuletzt das zeigt:
Machen wir doch einfach mal einen Teil einer Funktionsuntersuchung:

Quoted

[...]
Extrempunkte:
Notwendige Bedingung
f '(x)=0
f'(x) = e^x-2
e^x-2 = 0 |+2
e^x = 2 | ln
x = ln2 ~ 0.6931471805

An der Stelle ln2 ist möglicherweise eine Extrmstelle

Hinreichende Bedingung
f' (0) = e⁰-2 = -1
f' (ln2) = 0
f' (1) = e¹-2 = e-1 ~ +1.71

Es hat ein Vorzeichen wechsel von + nach - gegeben, daher handelt es sich an der Stelle x=ln2 um einen Tiefpunkt.

Y-Koordinate
f (ln2)= e^ln2 - 2 * ln2 = 2 - 2 * ln2 ~ 2 - 2 * 0.6931471805 ~ 1.386294361

[...]

Damit haben wir gezeigt, dass sich an der Koordinate (0.7/1.4) ein Tiefpunkt befindet, und es rechts und links von diesem nur nach oben entwickelt.
Zeig das Deinem Mathelehrer und sag ihm, dass es keine Nullstellen gibt.


p.s. Gefundene Rechtschreibfehler könnt ihr behalten. mathematische bitte ich zu korrigieren

Alle Klarheiten beseitigt? ;D

Quoted from "Sir_Flauschi28"

der lehrer wird doch wohl keine irrationale zahl gemeint haben? *horror*.

Ich denke nicht

dann hätte mir maple die als ergebnis ausgespuckt
also gibbet keine lösung *punkt*!